მათემატიკური ამოცანა რაგბზე

                         მათემატიკური ამოცანა რაგბზე

52-ე საჯარო სკოლის IXბ კლასის მოსწავლეებმა გააკეთეს პრეზენტაცია რაგბის შესახებ, რომელშიც ისაუბრეს იმაზე, თუ როგორ არის ყველაზე მოსახერხებელი მორაგბისთვის ლელოს დადება. ამისთვის მათ ამოხსნეს მათემატიკური ამოცანა.

ამოცანის პირობა:

გაეცანით ერთ-ერთი ულამაზესი და ვაჟკაცური სპორტული თამაშის - რაგბის წესებს.წრეწირთან დაკავშირებული კუთხეების(ჩახაზული კუთხე,მკვეთი კუთხე) თვისებების გამოყენებით,ახსენით:რატომ ცდილობს რაგბისტი ლელოს კარის ცენტრის ახლოს გატანას - იგი გარდასახვის წერტილთან არის დაკავშირებული

რაგბის წესების მიხედვით გარდასახვისა და ლელოს დადების წერტილები უნდა მდებარეობდენენ ერთ წრფეზე. ხოლო იმის დადგენა თუ რამდენი მეტრით  დაშორებული იქნება გარდასახვის წერტილი კარის ხაზიდან რაგბისტის გადასწყვეტია. რაგბისტები თავისი გამოცდილებით ადგენენ საუკეთესო დაშორებას კარის ხაზიდან და ზრდიან გარდასახვის განხორციელების ალბათობას. ჩვენ კი მოვუძებნით ამ ყველაფერს მათემატიკურ ახსნას.

განხილულია ორი შემთხვევა.

შემთხვევა 1.

ლელოს წერტილი მდებარეობს კარებს შორის.

CD- კარების სიგრძე(6 მეტრი)

AB-მანძილი ლელოს წერტილიდან გარდასახვის წერტილამდე

ტრიგონომეტრიის დახმარებით შეგვიძლია გამვთვალოთ ის კუთხე, რომლის ფარგლებში რაგბისტს შეუძლია გარდასახვის შესრულება. რაც დიდია კუთხე, მით მეტია გარდასახვის შესრულების ალბათობა.

ტანგენსი (tg) არის მოპირდაპირე და მიმდებარე კათეტების შეფარდება. ტანგენსის რიცხვითი მნიშვენელობის გარკვევის შემდეგ შესაძლებელია მისი საშუალებით შესაბამისი კუთხის დადგენა.

ჩვენ გვაინტერესებს კუთხე CBD. BC=BD, სამკუთხედი CBD ტოლფერდაა, აქედან გამომდინარე AB სიმაღლეცაა, ბისექტრისაც და მედიანაც. ამიტომ კუთხე CBD ორჯერ დიდია კუთხე CBA-ზე და კუთხე ABD-ზე.

1)      AB=10 მეტრი, კუთხე CBD=4 გრადუსი

2)      AB=20 მეტრი, კუთხე CBD=17 გრადუსი

3)      AB=30 მეტრი, კუთხე CBD=12 გრადუსი 20 მინუტი

4)      AB=40 მეტრი, კუთხე CBD=8 გრადუსი 40 მინუტი

შემთხვევა 2.

ლელოს დადების წერტილი დაშორებული კარებებიდან 28 და 34 მეტრით

ჩვენ გვაინტერესებს კუთხე ACB, მისი გამოთვლა შემდეგნაირად არის შესაძლებელი:

ACB=DAC – ABC ( რადგან კუთხე DAC სამკუთხედი ACB-ს გარე კუთხეა)

ამ შემთხვევაშიც ჩვენ შეგვიძლია გამუვთვალოთ კუთხეების DAC-ს და ABC-ს ტანგენსის დახმარებით გამოთვლა და მათი დახმარებით ჩვენთვის სასურველი კუთხის გაგება. შედეგები შემდეგია:

1)      CD=10 მეტრი, კუთხე ACB=3 გრადუსი 20 მინუტი

2)      CD=20 მეტრი, კუთხე ACB=5 გრადუსი

3)      CD=30 მეტრი, კუთხე ACB=5 გრადუსი 30 მინუტი

4)      CD=40 მეტრი, კუთხე ACB=5 გრადუსი 30 მინუტი

ამ გამოთვლების დახმარებით ვიგებთ რატომ ცდილობენ რაგბისტები ლელოს კარებებს შორის დადებას, გარდა ამის სხვადასხვა შემთხვევებში საუკეთესი დაშორებები, ასევე დადგინდა კანონზომიერება, რისი მიხედვითაც მანძილის გაზრდით თავიდან კუთხეც იზრდება, შემდეგ აჩერებს ზრდას და თითქმის იგივე რჩება, ბოლოს კი იწყებს კლებას. ეს რა თქმა უნდა ორივე შემთხვევაში სხვანაირად ვლინდება. პირველ შემთხვევაში ყველაფერი საგრძნობლად ხდება, მეორეში კი შედარებით ნელა.

ამის გარდა შეიძლება ამ ამოცანის უფრო სხვანაირად და მარტივად ამოხსნა, მაგრამ არა ასე დაწვრილებით.

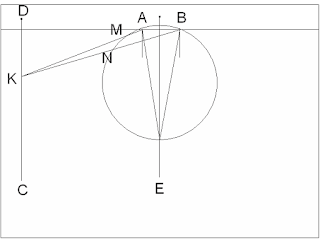
კუთხე AEB ჩახაზული კუთხეა და გამოითვლება AB რკალის ორზე გაყოფით, ხოლო კუთხე AKB მკვეთი კუთხეებია და არის AB და  MN რკალების სხვაობის ნახევარი.